Математическая модель точно описала отражение черными дырами Вселенной

Черные дыры — это компактные объекты, вокруг которых свет резко искривляется из-за кривизны пространства-времени. И хотя сам свет не может покинуть центральную массу за горизонтом событий, на больших расстояниях он может вращаться вокруг черной дыры. Этот феномен может позволить отдаленному наблюдателю видеть множественные версии одного и того же объекта. Несмотря на то, что этот факт известен уже на протяжении многих лет, у физиков-теоретиков только сейчас появилось точное математическое решение для этого явления. Исследование опубликовано в журнале Scientific Reports.

Вот что говорит Алберт Снеппен, студент Центра космического рассвета и Института Нильса Бора при Копенгагенском университете:

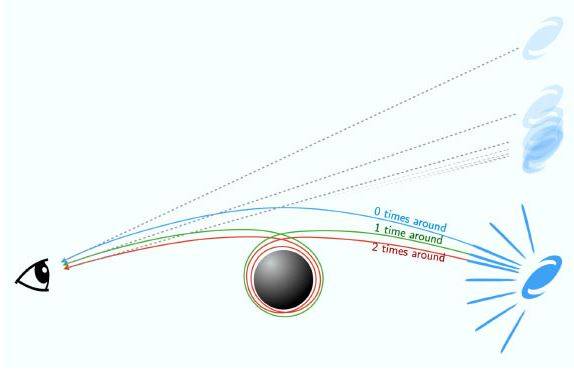
Далекая галактика светит во всех направлениях — часть ее света проходит вблизи с черной дырой и слегка отклоняется; часть света проходит еще ближе и обходит дыру один раз прежде, чем убежать в нашу сторону, и так далее. Наблюдая окрестности черной дыры, чем ближе к горизонту мы смотрим, тем больше одной и той же галактики мы видим.

Свет из фоновой галактики тем больше раз вращается вокруг черной дыры, чем ближе он проходит рядом с ней, таким образом наблюдатель видит одну и ту же галактику в нескольких направлениях. © Peter Laursen

Каждое следующее изображение находится в 500 раз ближе к ней, чем предыдущее — это известно уже более 40 лет. Однако до недавних пор вычисления были настолько сложными, что у ученых не было ни математической, ни физической интуиции относительно данного коэффициента.

Снеппен смог доказать, почему этот коэффициент именно такой при помощи простого численного и пертурбативного аналитического решения. Этот же метод можно применить и к вращающимся черным дырам.

Оказывается, при очень быстром вращении черной дыры вам уже не нужно приближаться к ней в 500 раз, а гораздо меньше.

Более того, каждое следующее изображение в этом случае теперь находится всего в 50, 5 или даже всего лишь в 2 раза ближе к краю черной дыры.

Алберт Снеппен

В случае со статичными черными дырами, когда каждое изображение находится в 500 раз ближе к горизонту событий, чем предыдущее, все они очень скоро «сжимаются» в одно изображение. Другими словами, множественные изображения очень сложно наблюдать в действительности. Однако, когда черная дыра вращается, то в ее окрестностях появляется больше места для дополнительных изображений. Снеппен надеется подтвердить свою теорию посредством наблюдений в ближайшем будущем.

Таким образом, мы можем изучать не только черные дыры, но и галактики, расположенные за ними. Чем больше свету приходится облетать черную дыру, тем больше увеличивается время его прохождения, так что изображения становятся все более запаздывающими. Если, например, в фоновой галактике звезда взрывается сверхновой, наблюдатель сможет видеть этот взрыв снова и снова.

Алберт Снеппен